2024年1月3日，美国化学会杂志The Journal of Physical Chemistry Letters在线发表了北京分子科学国家研究中心刘剑课题组题为“Nonadiabatic Field on Quantum Phase Space: A Century after Ehrenfest”的邀稿展望文章。该文旨在纪念约一个世纪前Ehrenfest夫妇一起提出相空间这一重要名词和Paul Ehrenfest提出著名的Ehrenfest定理，更重要的是为基于轨线的非绝热量子动力学方法发展提供一种崭新的思路。

　　由于原子核和电子的质量相差至少3个数量级，电子运动和原子核运动的时间尺度一般可以分离开来。这即是两位量子力学先驱Max Born和J. Robert Oppenheimer在1927年提出的Born-Oppenheimer近似，是一系列现代化学概念的基石。然而，当分子的不同电子态势能面相互靠近甚至出现简并的情况下，不同电子态之间的耦合变得不可忽略。这导致了Born-Oppenheimer近似的失效，使得体系允许在不同的电子态之间发生无辐射跃迁，形成非绝热过程。这一现象在化学、材料和生物学等领域的重要反应中起着关键作用，如光催化反应、电子转移、光合作用和光电转化等。为了更好地理解这些非绝热跃迁过程，人们迫切需要发展高效的非绝热动力学模拟方法。由于波函数方法计算成本的指数增长，轨线动力学成为模拟实际复杂分子体系非绝热动力学过程的主要方法。目前的轨线非绝热动力学方法主要包括基于1927年Ehrenfest定理思想的Ehrenfest（平均场）动力学和源于1970~1990年代John Tully工作的面跳跃动力学。尽管这些轨线动力学方法经过多年的发展取得了一定的成果，但仍然存在一些问题：Ehrenfest动力学在散射体系演化经历非绝热耦合区域至渐进区域无法准确描述原子核运动状态的分支现象，而面跳跃动力学虽然能处理好散射体系渐进区域的分支现象，但对于非绝热耦合区域范围广的（凝聚态）体系的动态行为描述有不小缺陷。在1911年Ehrenfest夫妇一起首次提出“相空间”（“Phasenraum”）这个名词百年之后，量子相空间表示理论逐渐被继续发展并用于开拓新的非绝热动力学理论，将有望提出更自洽的轨线动力学来解决这些问题，更好地同时描述电子和原子核的运动。　　

　　图1. (a): Paul Ehrenfest和Tatyana Ehrenfest夫妇（图片来源：Wikipedia）；(b): Ehrenfest夫妇提出相空间的原始文章(Ehrenfest;, P.; Ehrenfest, T. Begriffliche Grundlagen Der Statistischen Auffassung in Der Mechanik. In Encyklopädie Der Mathematischen Wissenschafte, B. G. Teubner: Liepzig,Germany, 1911; Vol. 4, pp 1-90)。

　　在这篇展望文章中，刘剑课题组提出了一种概念新颖的轨线动力学形式—非绝热场(nonadiabatic field, NAF)。这种动力学新方法把原子核的受力分为两部分，一部分为单一电子态势能面提供的力（称为绝热力），另一部分来自于非绝热耦合场贡献的部分（称为非绝热力）。NAF的提出旨在能够全面获取非绝热分子动力学中耦合区域和渐近区域的重要特征：在非绝热区域，原子核在单态势能面上运动的同时可以感受到电子相干反馈的非绝热力的贡献，使得NAF对体系在非绝热区域演化的描述更为准确。而当体系演化离开非绝热区域后，由于非绝热耦合自然消失，使得非绝热力的贡献也消失，NAF动力学自然退化为Born-Oppenheimer动力学形式，使得渐进区域原子核运动的分支效应得到合理描述。

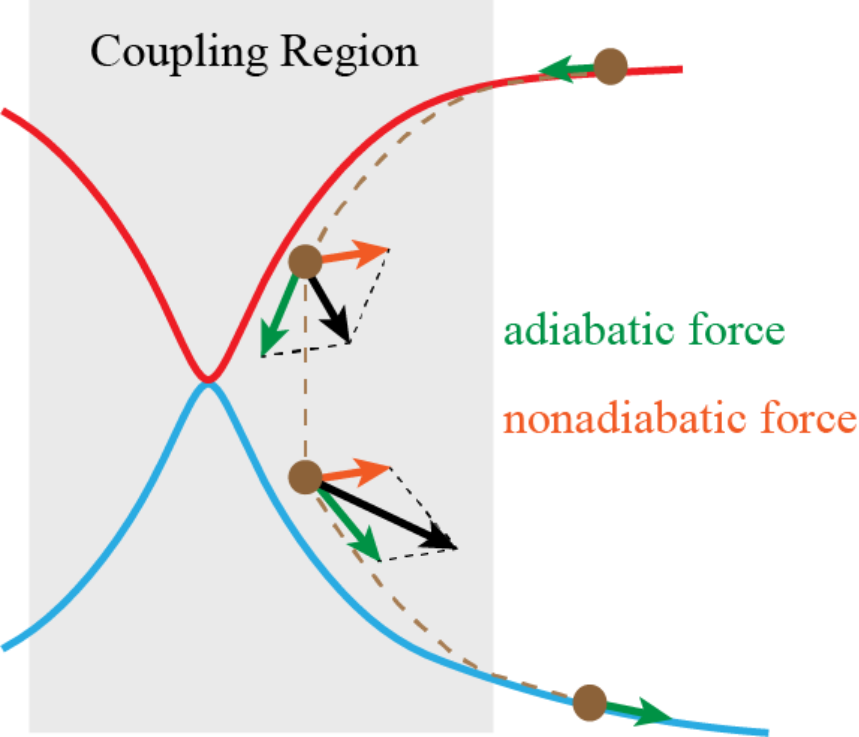
　　图2. NAF动力学的示意图

　　除了轨线运动方程外, 初始条件和计算物理量的积分形式是影响轨线动力学性能的另外两个重要因素。刘剑课题组将NAF轨线动力学应用于他们从2016年起建立的推广的量子力学相空间表示理论(The Journal of Chemical Physics, 2016, 145, 204105; The Journal of Chemical Physics, 2019, 151, 024105;The Journal of Physical Chemistry Letters, 2021, 12, 2496–2501; The Journal of Physical Chemistry A, 2021, 125, 6845–6863; Accounts of Chemical Research, 2021, 54, 4215–4228; Wiley Interdisciplinary Reviews Computational Molecular Science, 2022, 12, e1619)，其中原子核自由度由传统的Wigner位置-动量相空间描述，而电子自由度由约束（位置-动量）相空间刻画。电子自由度的约束相空间由布居数求和等于1这个物理条件确定，其数学结构可以关联到复Stiefel流形。结合量子力学相空间表示理论的初始条件和估计量的积分形式，NAF动力学在凝聚相耗散体系、光与物质相互作用模型、分子中的锥形交叉模型等体系的数值测试中，无论针对电子还是原子核的动力学性质，都展现出比传统Ehrenfest动力学和面跳跃方法更好的性能。研究同时表明NAF也可以在传统的Ehrenfest动力学或面跳跃动力学框架下直接系统地改进这两种方法的性能，然而因为这些传统方法中的初始条件和计算估计量的积分形式并不严格，所以对应的非绝热场方法远远不如基于严格的量子相空间表示理论的NAF。

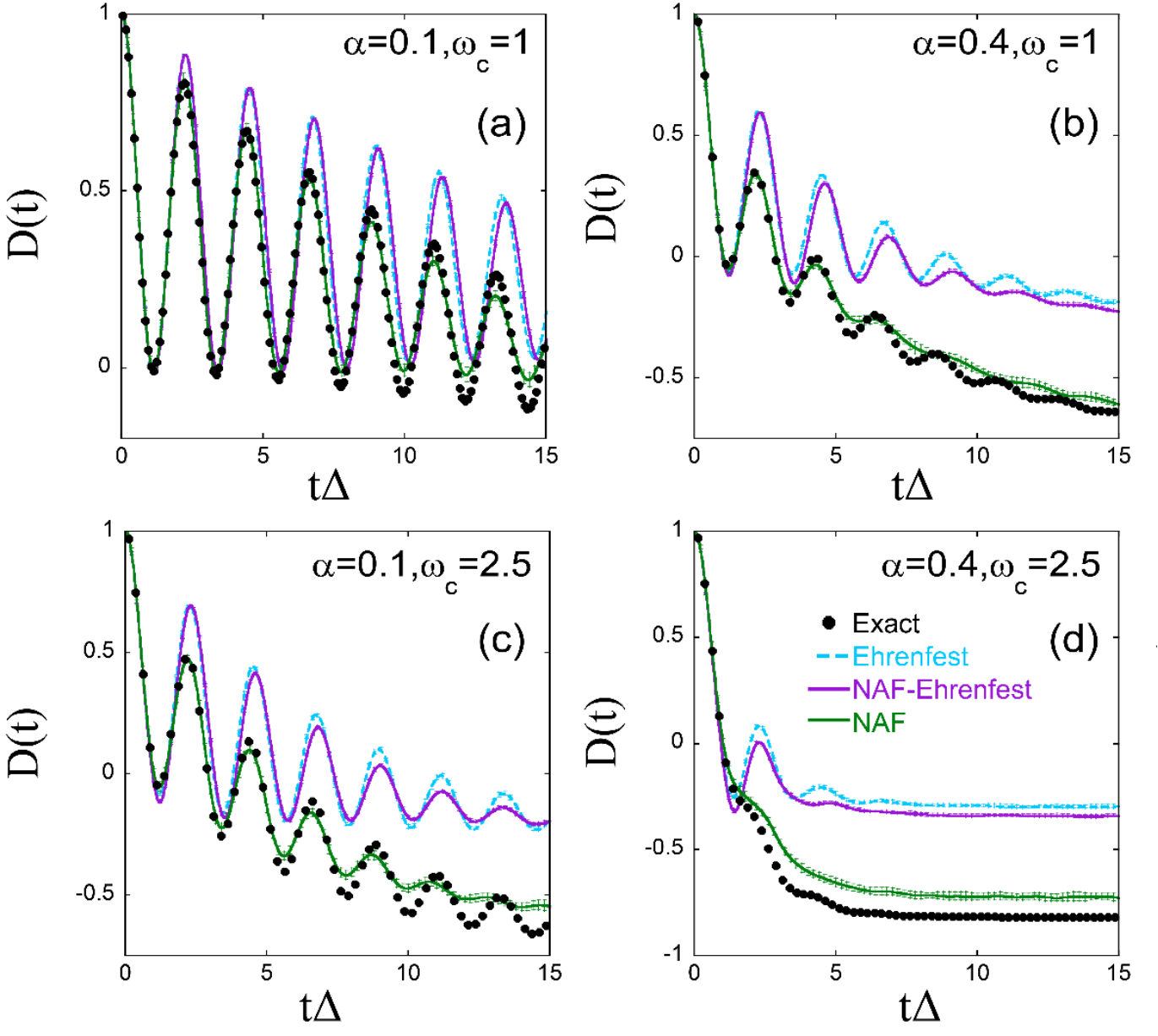
　　图3. Ohmic谱密度自旋玻色模型在低温(β=5)下两态布居数之差随时间变化的模拟结果。其中两态间的耦合为Δ=1，Kondo参数α和截断频率ωc分别为(a): α=0.1, ωc=1; (b): α=0.4, ωc=1; (c): α=0.1, ωc=2.5; (d): α=0.4, ωc=2.5。黑色圆点：量子力学的严格结果；青色虚线：Ehrenfest动力学的结果；紫色实线：NAF结合Ehrenfest动力学的结果；绿色实线：NAF结合量子相空间的结果。

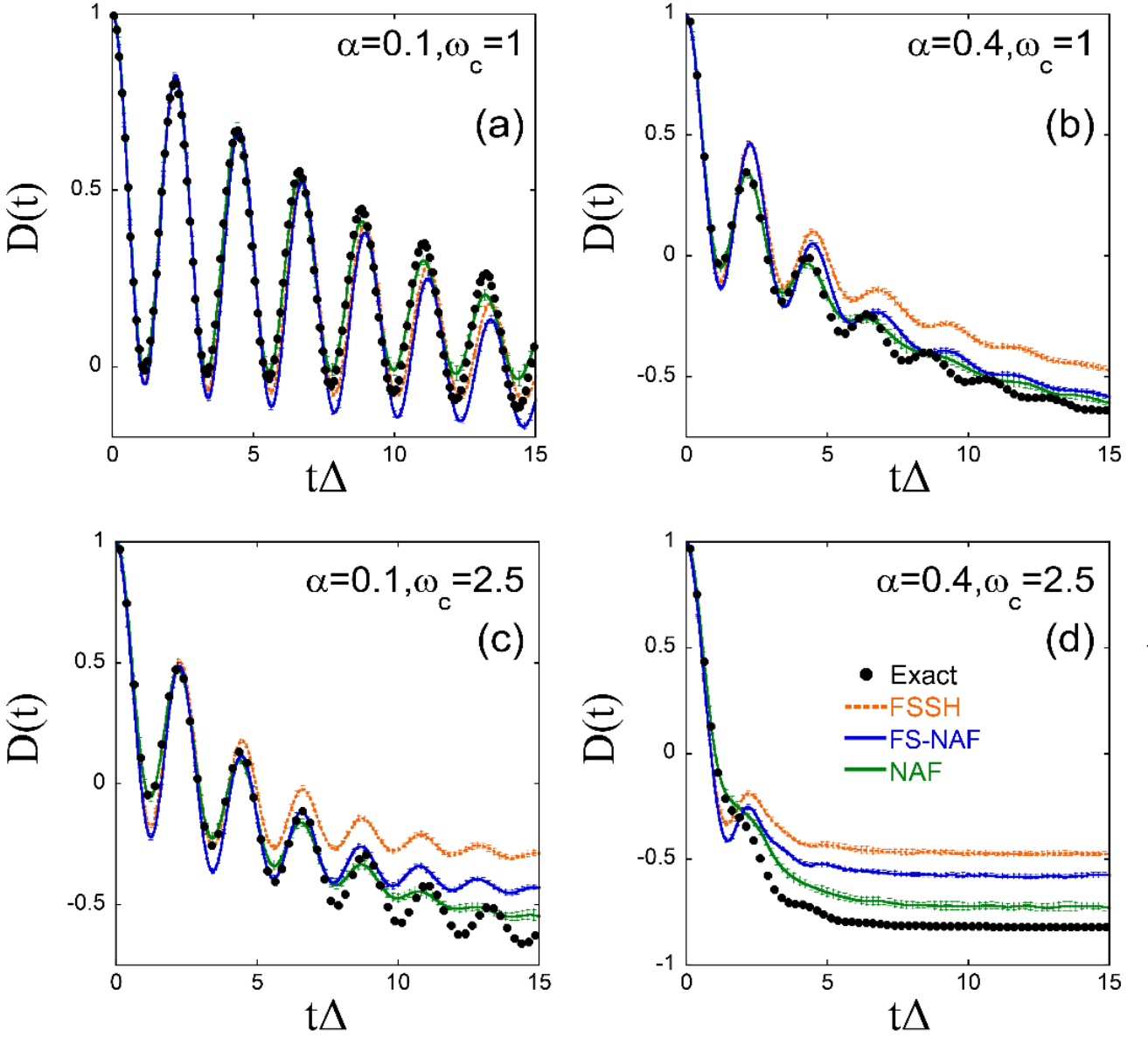
　　图4. Ohmic谱密度自旋玻色模型在低温(β=5)下两态布居数之差随时间变化的模拟结果。其中两态间的耦合为Δ=1，Kondo参数α和截断频率ωc分别为(a): α=0.1, ωc=1; (b): α=0.4, ωc=1; (c): α=0.1, ωc=2.5; (d): α=0.4, ωc=2.5。黑色圆点：量子力学的严格结果；橙色虚线：面跳跃方法的结果；蓝色实线：NAF结合面跳跃方法的结果；绿色实线：NAF结合量子相空间的结果。

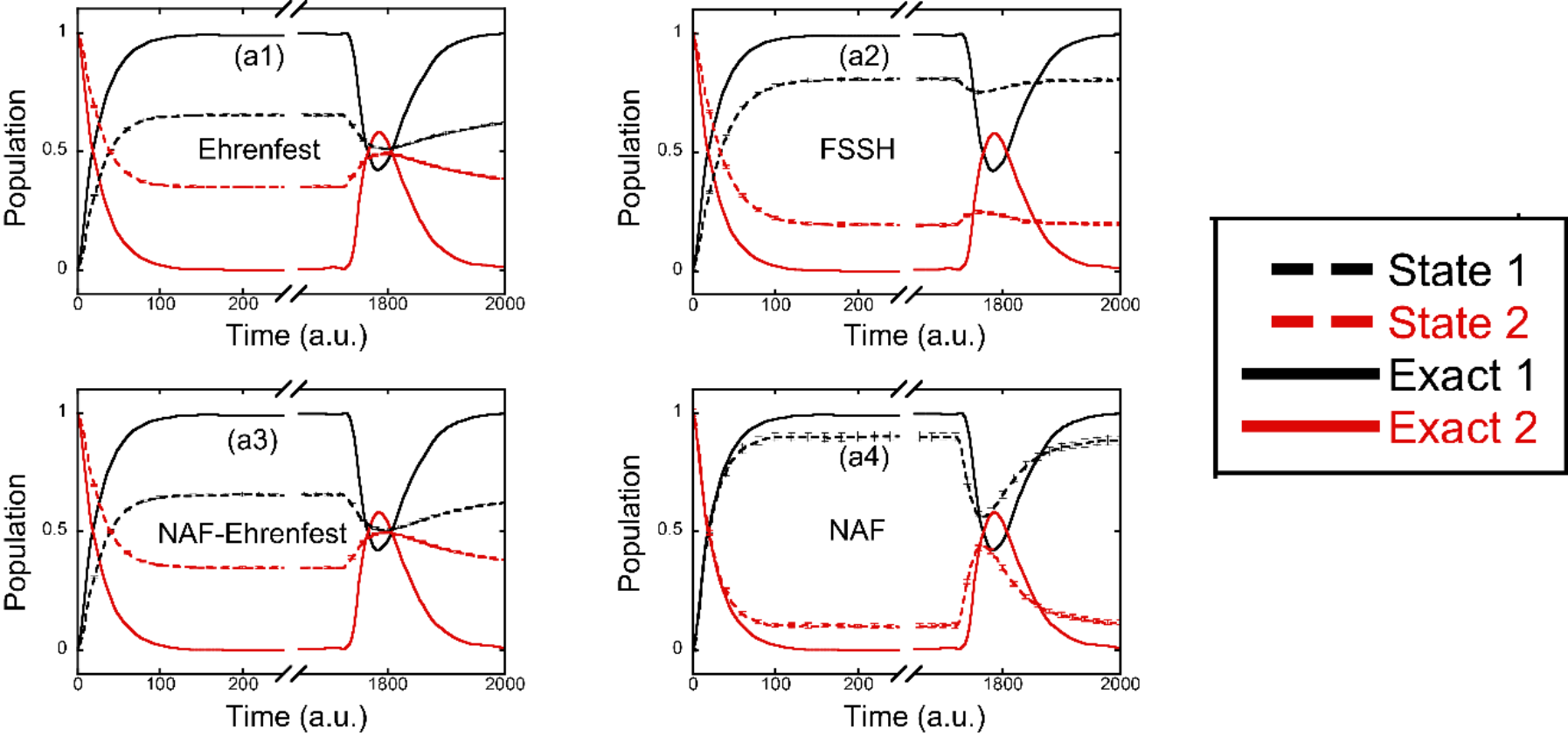
　　图5. 两态腔中原子模型的布居数动力学模拟结果。黑色和红色分别表示原子的基态和激发态布居数，实线和虚线分别表示量子力学的严格结果和轨线方法的模拟结果。(a1): Ehrenfest动力学的结果；(a2): 面跳跃方法的结果；(a3): NAF结合Ehrenfest动力学的结果；(a4): NAF结合量子相空间的结果。

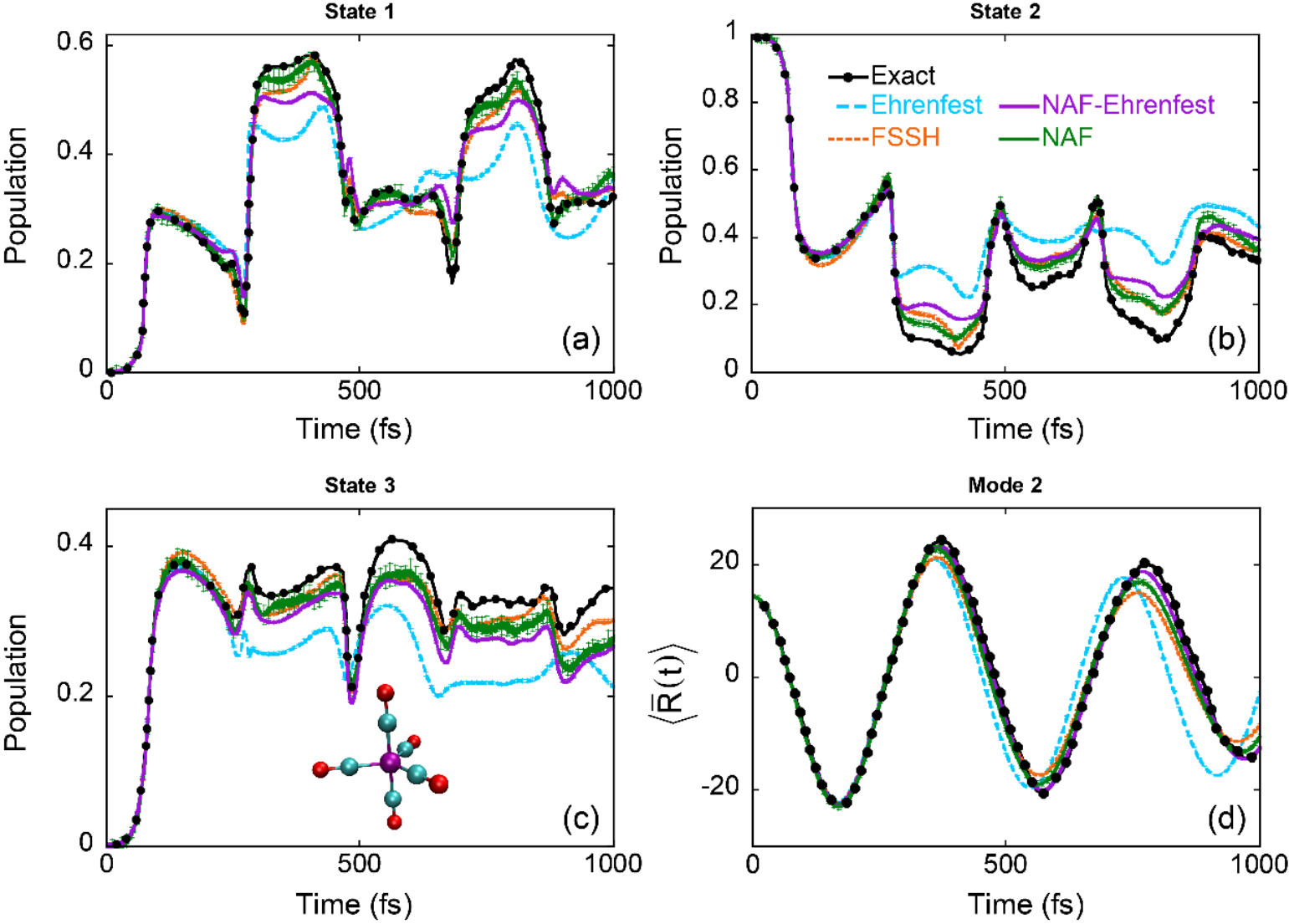
　　图6. Cr(CO)₅分子锥形交叉模型的模拟结果。(a)-(c): 各电子态的电子布居数随时间的变化；(d): 原子核位置随时间的变化。黑色点线：量子力学的严格结果；青色虚线：Ehrenfest动力学的结果；橙色虚线：面跳跃方法的结果；紫色实线：NAF结合Ehrenfest动力学的结果；绿色实线：NAF结合量子相空间的结果。

　　NAF具有平均场动力学和面跳跃动力学的各自优点，对体系在绝热区域和非绝热区域的运动都能合理描述。基于（约束）位置-动量相空间表示的量子理论，NAF在一系列非绝热体系的数值模拟中都表现更加优异。这一全新的轨线动力学方法将有望成为研究和模拟实际分子体系非绝热跃迁过程的有效工具，有助于人们深入了解复杂体系的光驱动化学过程。

　　北京大学化学与分子工程学院的博士研究生吴柏华和贺鑫为文章合作作者，刘剑教授为通讯作者。该工作得到了国家杰出青年科学基金项目(项目号: 22225304)的资助。计算资源由北京并行科技、广州超级计算中心以及北京大学高性能计算平台提供。

　　文章链接 “Nonadiabatic Field on Quantum Phase Space: A Century after Ehrenfest”

　　Baihua Wu, Xin He, Jian Liu*. The Journal of Physical Chemistry Letters. 2024, 15, 644−658